티스토리 뷰
추천 대회를 참여하면서, Neural Collaborative Filtering 모델을 경험했고, 해당 모델은 구조,내용상 어렵지 않아 논문을 발번역후 필자의 생각을 정리해보고자 한다.
논문 : https://arxiv.org/pdf/1708.05031.pdf
[서론]
최근 몇 년 동안, 심층 신경망은 음성 인식, 컴퓨터 비전 및 자연어 처리에서 엄청난 성공을 거두었다. 그러나 추천 시스템에 대한 심층 신경망의 탐색은 상대적으로 연구가 덜 되었다.
본 연구에서, 우리는 implicit 피드백을 기반으로 추천의 핵심 문제 (협업 필터링)를 해결하기 위해 신경망을 기반으로 한 기술을 개발하려고 노력한다.최근의 일부 연구는 추천을 위해 딥 러닝을 사용했지만, 주로 아이템의 텍스트 설명이나 음악의 음악 특징과 같은 보조 정보를 모델링하는 데 사용했다. 협업 필터링의 핵심 요소인 사용자와 항목 기능 간의 상호 작용을 모델링하는 데 있어 여전히 행렬 인수 분해에 의존하고 사용자와 항목의 잠재적 기능에 내적을 적용했다.
내적을 데이터로부터 임의의 기능을 학습할 수 있는 신경 아키텍처로 대체함으로써,우리는 NCF라는 이름의 일반적인 프레임워크를 제시한다. (NCF는 Neural network-based Collaborative Filtering 의 줄임말)
NCF는 일반적이며 프레임워크에서 행렬 인수 분해를 표현하고 일반화할 수 있다. 비선형성으로 NCF 모델링을 학습하기 위해 다층 퍼셉트론을 활용하여 user-item 상호 작용 함수를 학습할 것을 제안한다.두 개의 실제 데이터 세트에 대한 광범위한 실험은 최신 방법에 비해, NCF 프레임워크에서 상당한 개선을 보여준다. 경험적으로, 더 깊은 신경망을 사용하는 것이 더 나은 권장 성능을 제공한다는 것을 보여준다.
keywords
Collaborative Filtering, Neural Networks, Deep Learning, Matrix Factorization, Implicit Feedback
[ INTRODUCTION ] 소개
폭발적으로 정보가 넘쳐나는 시대에서, 추천 시스템은 정보 과부하를 완하하는 중심 역할을 하고, 전자 상거래, 온라인 뉴스 및 소셜 미디어 사이트를 포함한 많은 온라인 서비스에서 널리 채택되었다. 개인화된 추천 시스템의 핵심은 협업 필터링으로 알려진 과거 상호 작용(예: 등급 및 클릭)을 기반으로 항목에 대한 사용자의 선호도를 모델링하는 데 있다. 다양한 협업 필터링 기술 중 매트릭스 인수분해(MF)는 가장 인기있는 기술 중 하나며, MF는 user 또는 item을 공유된(동일한) 잠재 공간에 투영하고, 잠재 특징 백터를 사용하여 user나 item을 표현합니다. 그 후 user와 item의 상호작용은 그들의 잠재 백터를 내적하여 나타냅니다.
넷플릭스 대회를 통해 대중화된 MF는 잠재 요소 모델 기반 추천에 대한 접근 방식으로 받아들여졌다. 많은 연구자들은 MF를 발전시키기 위해 인접기반 모델과 통합, item 컨텐츠의 주제 모델과 결합, 특징의 일반 모델링을 위해 인수 분해 기계로 확장하는 방식으로 노력했다. 협업 필터링을 위한 MF의 효과에도 불구하고, 상호 작용 기능인 내적은 단순한 선택으로 인해 성능이 저해될 수 있다는 것은 잘 알려져 있다. 예를 들어 explicit feeback에 대한 등급 예측 작업의 경우 user와 item의 편향 요소를 내적을 통해 통합하여 MF 모델의 성능을 향상시킬 수 있다는 것은 잘 알려져 있다. 내적은 사소한 조정일 뿐이지만, 그것은 user와 item간 잠재적 특징 상호작용을 모델링하기 위해 더 나은 전용 상호작용 함수를 설계하는 긍정적인 효과를 나타낸다. 단순히 잠재피쳐를 선형적으로 곱하는 내적은 아마 복잡한 사용자 상호작용 데이터 구조를 충분히 포함할수 없을 수 있다.
이 논문은 이전의 많은 연구에서 수행된 내적이 아닌, 데이터에서 상호 작용 기능을 학습하기 위해 심층 신경망의 사용을 탐구한다.
신경망은 지속적인 기능을 근사화할 수 있는 것으로 입증되었으며, 최근에는 심층 신경망(DNN)이 컴퓨터 비전, 음성 인식에서 텍스트 처리에 이르는 여러 영역에서 효과적인 것으로 밝혀졌다. 그러나, MF 방식은 추천은 막대한 양의 문헌이 존재하는 반면 추천을 위해 DNN을 사용하는 작업은 상대적으로 적다. 비록 몇몇의 최근 발전된 방식에서 추천테스크에 DNN을 적용하여 좋은 결과를 보여주었지만, DNN 모델은 item의 텍스트 설명이나, 노래의 음악적 요소, 이미지의 시각적 컨텐츠와 같이 보조 정보를 나타내게 사용되었다. 핵심 협업 필터링 효과를 모델링하는 것과 관련하여 그들은 여전히 user와 item의 잠재인수를 내적하여 겨합하는 MF에 의존하였다.
본 연구는 협업 필터링을 위한 신경망 모델링 접근법을 공식화하여 앞서 언급한 연구 문제를 해결한다. 비디오를 보거나, 상품을 구매, 아이템 선택과 같은 사용자의 선호 행동을 간접적으로 반영하는 implicit feedback에 우리는 중점을 둔다. 명시적 피드백(즉, 시청률 및 리뷰)과 비교하여 암시적 피드백은 자동으로 추적될 수 있으므로 콘텐츠 제공자가 수집하기가 훨씬 쉽습니다. 그러나 사용자 만족도가 관찰되지 않고 부정적 피드백이 자연적으로 부족하기 때문에 활용하기가 더 어렵다. 본 논문에서는 DNN을 활용하여 노이즈가 많은 암시적 피드백 신호를 표현하는 방법의 중심 주제를 탐구한다.
이 논문에서 하고자 하는 것은 다음과 같다.
1. 우리는 user와 item의 잠재인수를 표현하는 신경망 아키텍쳐를 제시하고, 신경망 기반 협업 필터링을 위한 NCF 프레임워크를 고안한다.
2. 우리는 MF가 NCF의 부분으로 표현 될 수 있고 다층 퍼셉트론을 활용하여 NCF 모델링에 높은 수준의 비선형성을 부여할 수 있음을 보여준다.
3. 우리는 두개의 실제 데이터셋을 통해 우리의 NCF의 효과와 협업 필터링을 위한 딥러닝의 가능성을 입증하기 위해 광범위한 실험을 수행한다.
[PRELIMINARIES]
먼저 문제를 공식화하고 암묵적 피드백을 사용하여 협업 필터링을 위한 기존 솔루션에 대해 논의한다. 그런 다음 내적 사용으로 인한 한계를 강조하면서 널리 사용되는 MF 모델을 간략하게 요약합니다.
[Learning from Implicit Data]
M과 N은 각각 사용자, item을 나타낸다. 우리는 사용자-아이템 상호작용 행렬을 Y ∈ R^(M ×N)라 정의한다.
---- R^(MxN) = M x N행렬를 뜻함

(user와 item간 상호작용이 발견되면 1, 아니면 0을 가지는 y(ui))
여기서 y(ui) 1 값은 사용자 u와 항목 i 사이에 상호 작용이 있음을 나타냅니다. 하지만 실제로 i를 좋아한다는 뜻은 아닙니다.
마찬가지로, 값이 0이라고 해서 반드시 i를 좋아하지 않는 것은 아니며, 사용자가 항목을 인식하지 못하는 것일 수도 있습니다.
이러한 상황은 user의 선호도에 noise가 부여된 정보를 제공하기에 implicit data에서 학습하는데 어려움을 만든다.
관찰된 항목들은 적어도 아이템에 대한 유저의 흥미를 반영하지만, 관찰되지 않은 아이템들은 단지 누락 데이터일 수 있고, 자연스럽게 부정적 피드백이 부족하다.
implicit 피드백이 있는 추천 문제는 item의 순위를 매기는 데 사용되는 Y에서 관찰되지 않은 항목의 점수를 평가하는 문제로 공식화 될 수 있다. 모델 기반 접근법은 데이터가 모델에 의해 생성(또는 설명)될 수 있다고 가정한다. 형식적으로, 그것들은 y^ui = f (u, i|θ)를 학습하는 것으로 추상화될 수 있다. 여기서 y^ui는 상호작용의 예측점수를, θ는 모델의 파라미터, f는 모델 매개 변수를 예측 점수(우리가 상호 작용 함수라고 함)에 매핑하는 함수를 나타낸다.
매개 변수 Θ를 추정하기 위해 일반적으로 목적 함수를 최적화하는 기계 학습 패러다임을 따른다. pointwise loss, pairwise loss 두가지 목적 함수는 흔히 논문에서 가장 많이 사용되는 목적함수이다. 많은 양의 explicit 피드백의 정보로부터, pointwise 학습 방법은 대개 y^ui와 타겟값 yui 사이의 제곱손실을 최소화하는 회귀를 따른다. 부정적인 데이터의 부재를 처리하기 위하여 모든 관찰되지 않은 요소를 negative 피드백으로 다루거나, 관찰되지 않은 요소(item)중 일부를 샘플링한다. pairwise 학습의 경우, 관찰된 요소는 관찰되지 않은 어떠한 요소보다 높은 순위가 되야 한다는 아이디어다. 따라서, y^ui(예측값)와 yui(타겟값)사이의 loss를 최소화 시키는 대신, pairwise 학습은 y^ui와 yui의 마진을 최대화한다.
한걸음 더 나아가, 우리의 NCF프레임 워크는 신경망을 사용하여 상호 작용 함수를 매개 변수화하여 y^ui를 추정한다.
[2.2 Matrix Factorization] 행렬분해
MF는 각 user와 item을 잠재적 특징의 실제 값 벡터와 연결한다. pu는 사용자 u의 잠재백터, qi는 item i에 대한 잠재 벡터를 나타내도록 하자. MF는 yui를 pu와 qi의 내적으로 추정한다.

여기서 K는 잠재공간의 차원수를 나타낸다. 우리가 볼 수 있듯, MF는 잠재 공간의 각 차원이 서로 독립적이고 동일한 가중치로 선형 결합한다고 가정하여 사용자 및 항목 잠재 요인의 양방향 상호 작용을 모델링한다. 이와 같이, MF는 잠재적 요인의 선형 모델로 간주될 수 있다.
Figure1은 내적이 MF의 표현력을 제한할 수 있다는 것을 보여줍니다. 예를 잘 이해하기 위해서는 사전에 두 가지 설정을 명확히 해야 합니다. 첫째, MF는 user와 item을 동일한 잠재 공간에 매핑하기 때문에, 두 user 간의 유사성은 내적 또는 잠재 벡터 사이 코사인 각도로 측정할 수 있다. 둘째, 일반성의 손실 없이 MF가 복구해야 하는 두 사용자의 실제 유사성으로 jaccard 계수를 사용한다.
먼저 그림 1 a의 첫 번째 세 행(사용자)을 살펴보자. s23(0.66) > s12(0.5) > s13(0.4)을 알아내는 것은 쉽다.( 여기서 s23,s12,s13은 위에서 말함 jaccard 계수를 이용하여 구한 값임, //jaccard 계수 > ex) | u2 ∩ u3| / |u2 ∪ u3 | > 2/3 이므로 0.66) 이와 같이, 잠재 공간에서의 p1, p2, p3의 기하학적 관계는 Figure 1 (b)와 같이 표현할 수 있다. 이제 새로운 사용자 u4를 고려해 보자. 이 사용자의 입력은 Figure 1 (a)의 점선으로 표현했다. 우리는 s41(0.6) > s43(0.4) > s42(0.2)를 알 수 있는데, 이는 u4가 u1과 가장 비슷하고, 그 다음이 u3이고, 마지막이 u2라는 것을 의미한다. 그러나 MF 모델이 p4를 p1에 가장 가깝게 배치하는 경우(Figure 1 (b)에 두 가지 옵션이 점선으로 표시됨), p4는 p3보다 p2에 더 가까움, 이는 큰 순위 손실을 초래할 것이다.
저차원 잠재 공간에서, 복잡한 user 와 item간 상호작용을 추정하기 위해 단하고 고정된 내적을 방식을 사용하는 MF의 한계성을 위 예제를 통해 볼 수 있다. 우리는 이 문제를 해결하는 한 가지 방법이 많은 잠재적 요인 K를 사용하는 것이라 언급한다. 그러나 희소한 설정에서 모델의 일반화(예: 데이터 과적합)에 악영향을 미칠 수 있다. 본 논문에서는 DNN을 상호 작용 함수로 학습하여 한계를 해결한다.
[3. NEURAL COLLABORATIVE FILTERING]
우리는 먼저 암시적 데이터의 이진 특성을 강조하는 확률론적 모델로 NCF를 학습하는 방법을 자세히 설명하는 일반적인 NCF 프레임워크를 제시한다. 그런 다음 우리는 NCF에서 MF가 표현되고 일반화될 수 있음을 보여준다. 협업 필터링을 위한 DNN을 제안하기 위해, 우리는 user-item 상호 작용 함수를 학습하기 위해 다층 퍼셉트론(MLP)을 사용하는 NCF를 제안한다. 마지막으로 NCF 프레임워크에서 MF와 MLP를 결합하는 새로운 신경 행렬 인수 분해 모델을 제시한다. 이 모델은 user와 item 잠재 구조를 모델링하기 위한 MF의 선형성과 MLP의 비선형성의 장점을 통합한다.
[3.1 General Framework]
협업 필터링의 완전한 신경 처리를 하기 위해 Figure 2와 같이 다중 layer 표현을 채택하여 user-item간 상호 작용 yui를 모델링한다. 여기서 한 계층의 출력은 다음 계층의 입력 역할을 한다. 하단 입력 계층은 각각 user u와 item i를 설명하는 두 개의 피쳐 벡터 vu와 vi로 구성됩니다. 컨텐츠 인식, 컨텐츠 기반, 이웃 기반과 같은 사용자 및 항목의 광범위한 모델링을 지원하도록 사용자 정의할 수 있습니다. 이 작업은 순수한 협업 필터링 설정에 초점을 맞추고 있기 때문에 사용자와 item의 ID만 입력으로 사용하여 1-핫 인코딩을 한 2치화된 희소 벡터로 변환한다.이러한 입력에 대한 일반적인 피쳐 표현을 사용하면 콘텐츠 피쳐을 사용하여 user와 item을 표현함으로써 cold-start 문제를 해결하기 위해 우리의 방법을 쉽게 조정할 수 있다. (cold-start >> 추천문제에서 추천을 잘 해줄수 없는 문제)
입력 계층 위에는 임베딩 계층이 있다. 이것은 조밀한 벡터에 희소 표현을 투영하는 완전히 연결된 레이어이다. 임베딩 레이어를 통해 얻어진 사용자(item) 임베딩은 잠재 요인 모델의 맥락에서 사용자(item)에 대한 잠재 벡터로 볼 수 있다. user 임베딩과 item 임베딩은 우리가 neural collaborative filtering layer라 부르는 다층 neural 아키텍쳐를 통해 잠재 백터를 예측 점수로 매핑한다. neural CF 계층의 각 계층은 user-item 간 상호 작용의 특정 잠재 구조를 발견하도록 사용자 정의될 수 있다. 마지막 hidden 레이어 X의 차원수 따라 모델의 공정 능력이 결정됩니다. 마지막 출력층은 y^ui를 예측하며, 학습은 y^ui와 타겟값 yui 사이에 poitwise loss를 최소화하며 훈련을 수행한다. (poitwise > 제곱오차) 모델을 훈련하는 또 다른 방법은 베이지안 개인화된 순위 및 마진 기반 손실을 사용하는 것과 같은 pair wise 학습을 수행하는 것이다. 논문의 초점이 신경망 모델링 부분에 맞춰져 있기 때문에, 우리는 NCF의 pairwise 학습은 미래의 일로 남겨두겠다.
우리는 이제 NCF의 예측 모델을 공식화한다.
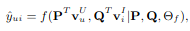

각 P는 user의 잠재인수 행렬, Q는 item의 잠재인수 행렬을 뜻하고, Θf는 상호작용 함수 f의 모델 파라미터를 의미한다.
함수 f는 다층 신경망으로 정의되기 때문에, 다음과 같이 공식화될 수 있다.
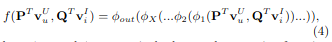
여기서 φout과 φx는 각각 출력층과 x번째 신경 협업 필터링(CF)층에 대한 매핑 함수를 나타내며, 총 X개의 신경 CF층이 있다.
3.1.1 Learning NCF
모델 매개 변수를 학습하기 위해 기존의 point-wise 방법은 주로 제곱 손실을 갖는 회귀 분석을 수행한다.

여기서 Y는 Y에서 관측된 상호작용의 집합을 나타내고, Y-는 관측되지 않은 상호작용의 모든 (또는 샘플링된) 음의 인스턴스의 집합을 나타낸다. 그리고 wui는 훈련 인스턴스(u, i)의 가중치를 나타내는 하이퍼 파라미터이다.(즉, layer다.) 제곱 손실은 관측치가 가우스 분포에서 생성된다고 가정하여 설명할 수 있지만, implicit 데이터와 잘 일치하지 않을 수 있다는 점을 우리는 지적한다. 그 이유로 implicit 데이터의 경우 타겟값 yui는 user u와 item i간 상호작용이 나타났는지 0과 1로 이진화하여 나타내기 때문입니다. 다음에서, 우리는 implicit 데이터의 이진 속성에 특별한 주의를 기울이는 point wise NCF를 학습하기 위한 확률론적 접근법을 제시한다.
implicit 피드백의 단일 클래스 특성을 고려하여 우리는 yui을 레이블로 볼 수 있다. yui가 1일때는 user와 item간 상호작용이 존재하고, 0일때는 상호작용이 존재하지 않는다는 것을 의미한다. 그런 다음 예측 점수 y^ui는 user와 item간 관련이 있을 가능성을 나타냅니다. NCF에 그러한 확률론적 설명을 부여하기 위해서는 출력 레이어 out에 대한 활성화 함수로 확률론적 함수(예: 로지스틱 또는 프로빗 함수)를 사용하여 쉽게 달성할 수 있는 [0, 1] 범위에서 출력 y^ui를 제한해야 한다. 위의 설정을 사용하여 likelihood 함수를 다음과 같이 정의합니다.


likelihood에 음수 로그를 고려하면, 우리는 위와 같은 식에 도달할 수 있다.
이는 NCF 방법에 대해 최소화하기 위한 목적 함수이며, 확률적 경사 하강(SGD)을 수행하여 최적화할 수 있다. 신중한 독자들은 그것이 로그 손실로도 알려진 이진 교차 엔트로피 손실과 같다는 것을 깨달았을 수 있다. NCF에 대한 확률론적 처리를 사용하여 우리는 implicit 피드백 추천을 이진 분류 문제로 해결하는 것으로 말하고있다. 분류 인식 로그 손실은 추천 논문에서 거의 연구되 않았기 때문에, 우리는 이 연구에서 이를 탐구하고 4.3절에서 그 효과를 경험적으로 보여준다. negative 인스턴스 Y-의 경우, 우리는 관찰되지 않은 상호 작용에서 균일하게 샘플링하고 관찰된 상호 작용의 수에 대한 샘플링 비율을 제어한다. 균일하지 않은 샘플링 전략(예: 항목 인기 편향)이 성능을 더욱 향상시킬 수 있지만, 우리는 탐색을 향후 연구로 남겨둔다.
[3.2 Generalized Matrix Factorization (GMF)]
이제 MF가 NCF 프레임워크의 특별한 경우로 해석될 수 있는 방법을 보여준다. MF는 가장 인기 있는 추천 모델이고 논문에서 광범위하게 조사되었기 때문에, 이를 재현할 수 있으면 NCF가 대규모 인수 분해 모델 제품군을 모방할 수 있다. 입력 계층의 user(item) ID의 원핫 인코딩으로 인해, 얻은 임베딩 벡터는 user(item)의 잠재 벡터로 볼 수 있다. 사용자 잠재백터는 pu(PTvu), item 잠재백터는 qi(=QTvi)로 칭한다. 우리는 첫 번째 신경 CF 층의 매핑 기능을 다음과 같이 정의한다.

(가운뎃점)은 element-wise product 를 뜻한다. 그런 다음 벡터를 출력 레이어에 투영합니다.

여기서 aout과 h는 각각 출력 레이어의 활성화 함수와 가중치를 나타낸다. 직관적으로, 우리가 aout에 대해 식별 함수를 사용하고 h가 1의 균일한 벡터가 되도록 강제한다면, 우리는 MF 모델을 정확하게 재현할 수 있다.
NCF 프레임워크 하에서 MF는 쉽게 일반화되고 확장될 수 있다. 예를 들어, 균일한 제약 조건 없이 데이터에서 h를 학습하도록 허용하면 잠재 차원의 다양한 중요성을 허용하는 MF의 변형이 발생할 것이다. 그리고 aout에 비선형 함수를 사용하면 MF를 선형 MF 모델보다 표현력이 더 높을 수 있는 비선형 설정으로 일반화합니다. 이 작업에서, 우리는 sigmoid 함수를 aout으로 사용하고 로그 손실이 있는 데이터에서 h를 학습하는 NCF 안에서 일반화된 버전의 MF를 구현한다(섹션 3.1.1). 우리는 그것을 GMF, 일반화된 행렬 인수 분해의 줄임말로 부른다.
[3.3 Multi-Layer Perceptron (MLP)]
NCF는 user와 item을 두가지 방식으로 모델링하기 때문에 두 경로를 통해 나온 피쳐를 합쳐서 결합시켜야 합니다. 이러한 설계는 멀티 모달 딥러닝 작업에서 널리 채택되었다. 그러나 단순히 벡터 연결은 사용자와 항목 잠재 기능 간의 상호 작용을 설명하지 않으므로 협업 필터링 효과를 모델링하기에 충분하지 않다. 이 문제를 해결하기 위해, 우리는 user와 item 잠재 기능 간의 상호 작용을 학습하기 위해 표준 MLP를 사용하여 연결 벡터에 숨겨진 레이어를 추가할 것을 제안한다. 이러한 의미에서, 우리는 고정된 element-wise곱을 하는 GMF 방식보다 user와 item간 상호작용을 학습하는데 더 큰 수준의 유연성과, 비선형성을부여할 수 있다.더 정확히 말하자면, 우리의 NCF에 포함된 MLP모델을 이와같이 정의된다.

여기서 Wx, bx 및 ax는 각각 x번째 층의 퍼셉트론에 대한 가중치 행렬, 바이어스 벡터 및 활성화 함수를 나타낸다. MLP 층의 activation function의 경우, sigmoid, tanh, ReLU를 선택할 수 있다. 우리는 각 function을 분석하고 싶다. 1) 시그모이드 함수는 각 뉴런의 출력을 (0,1) 사이로 제한하는데, 이는 모델의 성능을 제한할 수 있다, 출력이 0 또는 1에 가까울 때 뉴런이 학습을 중단하는 것으로 알려져 있다(기울기 손실). 2) tanh는 더 나은 선택이고 널리 채택되었음에도 불구하고, sigmoid의 축소판(tanh(x/2) = 2π(x) - 1)으로 볼 수 있기 때문에 시그모이드의 문제를 어느 정도 완화시킬 뿐이다. 3) 따라서 더 타당하고 불포화인 것으로 입증된 ReLU를 선택한다. 더욱이 희소 활성화를 촉진하고 희소 데이터에 잘 적합하고 모델이 과적합될 가능성이 낮다. 우리의 경험적 결과는 ReLU가 tanh보다 약간 더 나은 성능을 산출하며, 이는 다시 sigmoid보다 상당히 우수하다는 것을 보여준다.
네트워크 구조 설계의 경우, 공통적인 해결책은 아래 층이 가장 넓고 각 연속 층이 더 적은 수의 뉴런을 갖는 타워 패턴을 따르는 것이다(Figure 2 참조). 전제는 상위 layer에서 소수의 히든 유닛을 사용하여 모델은 데이터의 추상적인 특징을 배울 수 있다는 것이다. 우리는 모델의 구조를 경험적으로 연속적인 각 상위 계층에 대한 크기를 절반으로 줄여 구현하였다.
[3.4 Fusion of GMF and MLP]
지금까지 우리는 NCF의 두 가지 인스턴스를 개발했다. 선형 커널을 적용하여 잠재적 특징 상호 작용을 모델링하는 GMF와 비선형 커널을 사용하여 데이터에서 상호 작용 기능을 학습하는 MLP이다. 그런 다음 어떻게 NCF 프레임워크에서 GMF와 MLP를 결합하여 복잡한 user-item 상호 작용을 더 잘 모델링하기 위해 왜 서로를 강화할 수 있는지에 대한 질문이 발생한다.
간단한 해결책은 GMF와 MLP가 동일한 임베딩 레이어를 공유하도록 한 다음 상호 작용 함수의 출력을 결합하는 것이다. 이러한 방식은 잘 알려진 신경 텐서 네트워크(NTN)와 유사한 방식이다. 구체적으로, GMF와 단층 MLP를 결합하는 모델은 다음과 같이 공식화될 수 있다.
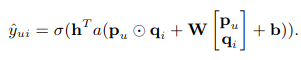
그러나 GMF와 MLP의 임베딩을 공유하면 융합 모델의 성능이 제한될 수 있다. 예를 들어, GMF와 MLP는 동일한 크기의 임베딩을 사용해야 한다는 것을 의미한다. 두 모델의 최적 임베딩 크기가 크게 달라지는 데이터 세트의 경우 이 솔루션은 최적의 결합을 얻지 못할 수 있다. 융합 모델에 더 많은 유연성을 제공하기 위해 GMF와 MLP가 별도의 임베딩을 학습하고 마지막 숨겨진 레이어를 연결하여 두 모델을 결합할 수 있도록 한다. Figure 3은 다우리의 제안이며, 밑에 식으로 공식화 할 수 있다.

여기서 pGu 및 pMu는 각각 GMF 및 MLP에서 user 임베딩을 나타낸다. qGi 와 qMi는 item 임베딩을 나타낸다.
앞에서 논의한 바와 같이, 우리는 MLP 층의 활성화 기능으로 ReLU를 사용한다. 이 모델은 사용자 항목 잠재 구조를 모델링하기 위해 MF의 선형성과 DNN의 비선형성을 결합한다. 우리는 이 모델을 Neural Matrix Factorization의 줄임말인 "NeuMF"라고 부른다. 각 모델의 파라미터들은 일반적인 오차역전파로 인해 계산될 수 있지만, 공간의 제한으로 여기서는 생략한다.
[3.4.1 Pre-training]
NeuMF의 목적 함수의 non-convexity(비볼록성)으로 인해 그레이디언트 기반 최적화 방법은 로컬 최적 솔루션만 찾는다. 초기화는 딥 러닝 모델의 융합과 성능에 중요한 역할을 하는 것으로 보고되었다. NeuMF는 GMF와 MLP의 앙상블이기 때문에, 우리는 GMF와 MLP의 사전 훈련된 모델을 사용하여 NeuMF를 초기화할 것을 제안한다. 우리는 먼저 수렴할 때까지 무작위 초기화로 GMF와 MLP를 훈련시킨다. 그런 다음 NeuMF에서 해당 부분에 대한 초기값으로 사용합니다. 유일한 조정은 출력 레이어에서 우리가 두 모델의 가중치를 연결하는 것이다.
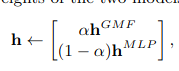
여기서 hGMF와 hMLP는 각각 사전 훈련된 GMF와 MLP 모델의 h 벡터를 나타내며, α는 두 사전 훈련된 모델 사이의 균형을 결정하는 하이퍼파라미터 변수이다.
GMF와 MLP를 처음부터 훈련하기 위해, 우리는 빈도가 낮은 매개 변수에 대한 빈번한 업데이트와 대규모 업데이트를 수행하여 각 매개 변수에 대한 학습 속도를 조정하는 Adam을 채택한다. Adam 방법은 바닐라 SGD보다 두 모델 모두에 대해 더 빠른 수렴을 생성하고 학습률을 조정하는 시도를 줄인다. NeuMF에 사전 훈련된 매개 변수를 공급한 후 Adam 대신 바닐라 SGD로 최적화한다. 이것은 Adam은 매개변수를 올바르게 업데이트하기 위해 모멘텀 정보를 저장해야 하기 때문이다. 사전 훈련된 모델 매개 변수로만 NeuMF를 초기화하고 momentum imformation(운동량 정보)를 저장하지 않기 때문에 운동량 기반 방법으로 NeuMF를 더 최적화하는 것은 적절하지 않다.(즉, Adam이 적절치 않다)
=====================================================================================
이 이후는 실험에 관련된 내용이므로 생략하겠다.
다음 포스트는 해당 논문의 대한 정리와 필자의 생각을 써보겠다!
- Total
- Today
- Yesterday
- 오블완
- CNN
- GIT
- yolov11
- YOLOv8
- YOLO
- 정리
- 오류
- 파이썬
- 깃
- github
- 욜로
- V11
- java
- DeepLearning
- 초보자
- 어탠션
- 뜯어보기
- GNN
- 자바
- python
- Tree
- LLM
- 도커
- 이미지
- c3k2
- docker
- 티스토리챌린지
- 알고리즘
- 딥러닝
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
