티스토리 뷰
해당 강의를 참고하여 공부하였습니다.
https://www.youtube.com/watch?v=4C8SUZJPlMY
기존 GBM은 모든 feature, 모든 객체(row)에 대해 Scan을 진행하여 imformation gain을 측정해야 하기때문에, 시간적으로 오래 걸리며, sequential함. ( parallel 하지못함.)
위와같은 시간적 문제점을 해결하기 위해 XGBoost는 Bucket이라 부르는 단위로 쪼갠 후 Bucket안에 있는 데이터의 information gain을 측정하여 최적의 split을 approximate하는 방식을 사용하여 parallel할 수 있도록 만듬. > 모든 data instance을 스캔하는 것을 완하시켜 속도를 빠르게 함.
Bucket = HistoGram-based
그에반에 LGBM은 다른 방식으로 접근하려 함.
GOSS (Gradient - based One - Side Sampling) > 모든 data point(row)를 스캔하지 않기위한 방법
> 개별적인 데이터들은 각각 다른 Gradient를 가지고 있으며, Gradient가 크면 클수록 더 중요한 객체(학습이 잘 안된 것)가 된다.
결국, Gradient가 큰 객체들은 남기고, Gradient가 작은 객체들은 random하게 drop를 하여 갯수를 줄인다.

위 사진과 같이 GOSS는 Large Gradient는 모두 사용하며, Small Gradient는 Random하게 Sampling하여 사용한다.
GOSS는 간단한 내용.
단 , 1 - a / b 가 >1 이면, GOSS의 의도를 극대화 할 수 있다고 한다.
그런데 중요한건.. LGBM default는 GBDT ( Gradient Boosting Decision Tree)를 사용함.. GOSS는 선택할 수 있음, DART도 있음
즉, sparse한 space가 많다면.. GOSS를 사용해야 하는 것 같다. ( 필자 생각)
===========================================================================================
EFB ( Exclusive Feature Bungdling) > 모든 feature들에 대해서 수행하지 않기 위한 방법
가정. one-hot encoding과 같이 feature space가 매우 sparse한 경우에는 굉장히 많은 feature들이 거의 exclusive하다.
의미 :하나의 객체에 대해서 특정한 두 변수(feature)가 전부 0이 아닌 값을 동시에 가질 경우가 드물다.
Exclusive한 feature들을 하나의 변수로 만들겠다. > 문제점 : 간혹가다 feature들이 Exclusive 하지 않을 경우에는 약간의 오류가 있을 가능성을 가지고 가는것.
완벽하게 Exclusive한 데이터들은 Bundling하여도 , performance는 떨어지지 않는다.
Exclusive하다는 건 무엇일까??? : 다들 XOR (Exclusive OR)을 들어봤을 것이다. 여기서 Exclusive란, 상호배타적 즉, 둘 중 하나의 값이 없는 경우를 말한다. (e.g. feature 1 : 1 , feaute 2: 0 일 경우 Exclusive)
즉, LGBM도 이러한 Exclusive한 feature들을 묶어서 압축하겠다는 의미같다. 하지만, 이렇게 처리를 하게 되면 문제가 생기게된다. 늘 항상 Exclusive한 경우가 나오지 않을 경우가 생긴다.( 밑에 예시가 있다.)
그래서, 약간의 오류가 생길 가능성은 있지만, feature를 줄일 수 있어서 속도를 향상시킬 수 있다.
그럼 어떻게 Bundling하고 압축하는지 알아보자.
절차 1.
Greedy Bundling
지금 현재 존재하는 feature set에 대해서 어떠한 feature들을 하나의 Bundle로 묶을 것인지 결정,
- Graph coloring problem으로 표현 가능함.
V : feature
E : 두 featurer간의 conflicts ( Conflict가 많은 경우는 Bundling되면 안됨. > 중복이 많다는 의미 ,즉 Exclusive하지 않는 부분이 많다)
e.g. conflicts를 정의하는 기준 > 동시에 none zero 값을 가지는 비율
즉, conflicts가 없는( 적은 ) feature들끼리는 Bundling해도 되는 것! > Exclusive한 데이터 셋을 가지고 있기때문에 하나의 feature로 만들어도 많은 양의 정보를 그대로 유지할 수 있음.

위 사진은 Greedy bundling의 예시다.
각 feature(node)별 얼마나 conflict가 존재하는지, 총 degree(모든 노드에 대한 conflict)를 구하게 된다.
총 degree를 구하는 이유는, Greedy 알고리즘으로 간선 삭제의 시작점(노드)을 설정하기 위한것이다.

그래프로 표현하게 되면, 위와같은 그래프를 그릴 수 있다. 이 그래프를 이용하여 정해놓은 cut-off를 기준으로 간선(E)를 없앤다.
현재 Cut-off는 0.2며, N은 10이기 때문에 간선(E, conflincts)가 2이상인 간선을 제거한다.

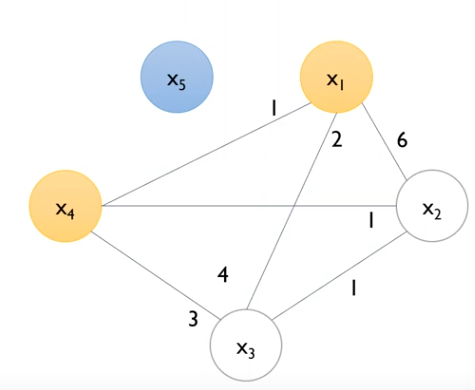

위 사진들은 Bundle로 묶을 feature를 선택하기 위해 간선 제거 과정이다.
X5는 모든 V(feature)에 E(conflict)가 2 이상이므로 단독으로 사용된다. 즉, X5는 모든 feature와 Conflict가 높아 묶지 말아야 한다.
그 후 , x1은 x4와 연결되며 다른 (x2,x3)와는 연결이 끊긴다. x1와 연결된 x4는 x2와 연결되지만, 이미 x1와 끊겼기때문에 맨 오른쪽 사진처럼 되는것이다.
결과적으로, {x5},{x4,x1},{x2,x3} 총 3개의 bundle로 바꿀 수 있다는 소리다. = 5개의 feature를 3개로 줄이겠다! > 속도 UP!!!
이렇게 Bundeling을 수행하고 난 후 하나의 feature로 만들게 된다.
절차 2.
Merge Exclusive Features - Greedy Bundling을 한 후, 하나의 변수로 표현하는 알고리즘
Greedy Bundling을 했지만, 어떻게 n개의 feature를 1개의 변수로 바꿀것인가?
LGBM은 각 Bundle로 구성되는 feature들 중 기준이 되는 feature의 최소, 최대값을 구해 기준점으로 삼은 후 새로운 feature로 변환시키는 방식을 사용한다. 말로는 어려우니 밑의 예제를 보면 단번에 이해가 가능할 것이다.


현재 {x5} , {x1,x4} ,{x2,x3}를 Bundling한 상황이고, 이것을 하나의 변수로 바꿔보도록 해보자.
{x1,x4}를 살펴보자.
1. x1이 기준점이 되며, x1의 max값을 구한다.
2. row별로, x1과 x4의 합을 구한다.
-2.1 만약, x1 = N, x4 = 0 이면, 단순 합을 통해 구한다. ( x1 + x4 )
-2.2 만약, x1 = 0, x4 = N 일때, x1 Max값 + x4값을 구한다. ( Max(x1) + x4 )
-2.3 만약, x1 = N , x4 = N 일때, x1의 값을 사용함. ( x1 )
-2.4 만약, x1 = 0 , x 4 = 0 일때, 0값 사용 ( 0 )
이와같은 방식을 취하여 변수 값을 변경하여 하나의 변수로 압축하는 과정을 거친다.
또 lgbm은 leaf-wise tree를 구성한다고 한다..


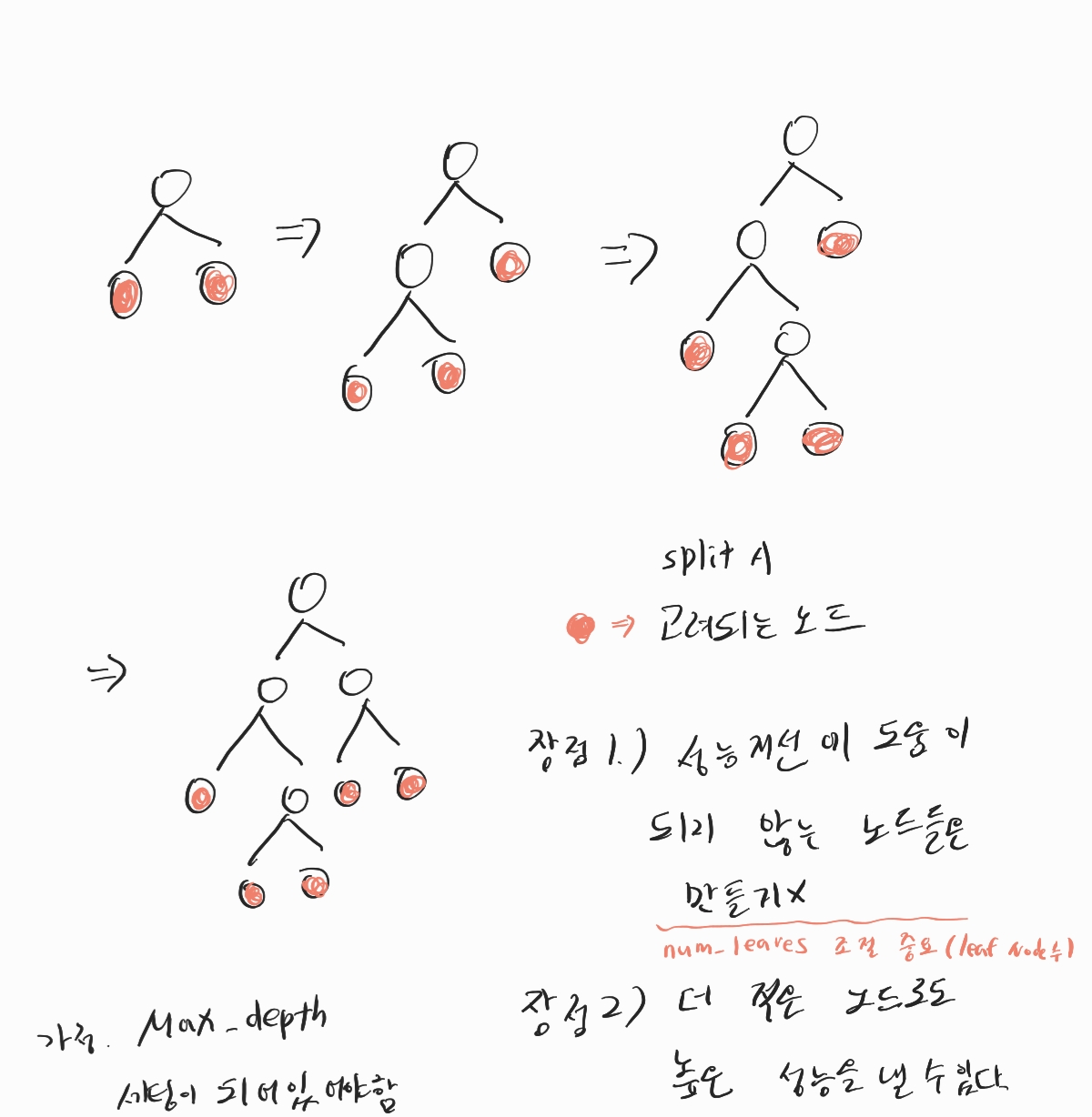
leaf wise tree의 아이디어는.. 각 leaf node중 가장 IG가 높은 leaf노드를 선택하여 그 노드를 split시킨다.
그 후 다시 모든 leaf중 IG가 높은 node를 선택하여 트리를 확장해나간다.
중요 파라미터
max_depth : 4 ~ 15
num_leaves : tree가 가질 수 있는 최대 leaf노드 수 ( 31, 63, 127, 255, 511 ... 2의 거듭제곱 -1 )
> 보통 트리 구조상 생길 수 있는 leaf_node를 가질 수 있는 수
min_child_samples( 특히, regression ) : leaf node가 되는 최소 데이터 sample 수
ex) leaf node의 최소 샘플수니.. 50개중 10 , 40 으로 스플릿 x > 다음 best를 찾음.
colsample_bytree : 0.5 ~ 0.8
reg_labmda : 0.1 ~ 20 (키울 수록 overfitting 방지 )
n_estimators : 50 ~ 2000
learning_rate : 0.1 , 0.01, 0.001
'머신러닝' 카테고리의 다른 글
| [ML] iForest / Extended iForest 정리 (0) | 2023.04.29 |
|---|---|
| [ML] XGBoost 기본 정리 (0) | 2023.04.09 |
| [ML] MCD ( Minimum Covariance Determinent ) - 2. MCD모델 원리 (0) | 2023.03.31 |
| [ML] MCD ( Minimum Covariance Determinent ) - 1. 마할라노비스 거리 (Mahalanobis distances) (0) | 2023.03.26 |
| [ML] GBM(Gradient Boosting Machine) - (2) Regressor 손으로 구하기 (0) | 2023.03.23 |
- Total
- Today
- Yesterday
- 초보자
- github
- YOLO
- 이미지
- 딥러닝
- LLM
- 정리
- 깃
- docker
- V11
- java
- 오류
- 티스토리챌린지
- YOLOv8
- 뜯어보기
- yolov11
- c3k2
- GNN
- 도커
- CNN
- python
- 자바
- DeepLearning
- 파이썬
- GIT
- 욜로
- 알고리즘
- Tree
- 어탠션
- 오블완
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
