티스토리 뷰
이번 포스팅에서는 Bagging방식의 앙상블과 양대산맥을 이루는 Boosting 앙상블 방식을 사용하는 Ada(아다)Boosting을 한번 살펴보려고 한다.
들어가기 전에.. DT(Decision Tree)에 대해 자세히 알고있으면 좋으므로, 공부를 하고 보는 것을 추천한다.
https://sims-solve.tistory.com/88
[ML] 의사결정트리(Decision Tree) 정리
의사결정트리는 Forest 계열에 가장 base로 사용되는 모델이다. RandomForest , Extra Tree, 일부 Boosting계열 모델에서 n개의 decision tree가 사용되므로 의사결정 트리를 상세하고 정확하게 공부하고 넘어가
sims-solve.tistory.com
1) Boosting이란?
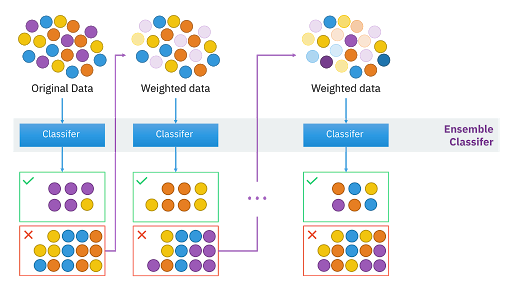
Boosting을 공부하다 보면 [그림 1]과 같은 이미지를 많이 봤을 것이다.
Boosting은 판별기가 잘못 판별한 sample의 weight(가중치)를 바꾼 후, 다음 판별기에 input으로 넣어 이전에 맞추지 못했던 데이터를 보다 잘 맞출 수 있는 판별기를 만드는 것이다.
이렇게 만들어진 n개의 판별기에 가중치를 곱한 후, 앙상블하여 최종 결과를 출력하게 된다.
물론, 각 판별기는 정확도가 51%이상 되야 의미가 있다.(2진분류 일때라 가정)
왜냐하면, 51%미만일시 단순히 찍는 수준의 성능이기 때문에 앙상블을 하더라도 성능이 좋아지지 않는다.
그래서, Boosting에서는 찍는것보다 높은 수준의 분류기만 사용하게 된다.
Boosting에서 알아둬야 할 단어가 몇가지 있다.
1. Sequential
2. sample_weight
3. estimator_weight
이 세 단어가 가장 중요하다고 개인적으로 생각한다.
1. Sequential
Sequential은 '연속적인'이라는 단어다. Boosting은 판별기1의 결과를 바탕으로, data sample weight를 변경하여 판별기2의 input으로 사용하고, 판별기2의 결과를 바탕으로 다시 data sample weight를 변경하여 판별기3의 input으로 사용한다.
즉, n개의 판별기를 연속적,순차적으로 거치면서, 잘 못 분류하는 data sample의 가중치를 Boost하면서 진행한다.
그래서 Sequential 이라는 소리를 하는 것이다.
반면에, RF(Random Forest)는 parallel 이라고 한다. n개의 복원추출 데이터 셋을 독립적으로 만들어 진행하여, 각각의 Tree는 영향을 전혀 받지 않기 때문이다.
2. sample_weight
Boosting이나 Bagging이나 둘 모두 sample_weight의 존재는 아주 중요하다.
사실.. Boosting, Bagging을 할때 확률적으로 데이터셋을 추출 후 구성하여 학습을 진행한다고 많이들 설명하지만, sklearn을 디버깅해보면 사실 두 방식 모두 모든 데이터 셋을 사용하는데, 각 sample_weight를 변경하여 Gini계수 값을 구할때 영향력을 바꾸는 것이다. 즉, 새로운 데이터 셋을 구성하는게 아닌 Gini계수를 구할때 데이터 셋의 영향력을 줄이고,늘려 마치 새로운 데이터셋을 보는 것처럼 하는 방식이다.
Boosting에서는 이러한 sample_weight가 다음 tree에 영향을 주기때문에 아주 중요하다고 할 수 있다.
3. estimator_weight
estimator_weight는 판별기가 얼마나 앙상블할때 얼만큼의 영향을 미칠지 나타내는 것이다.
N개의 판별기중 보다 성능이 우수한 것은 많이 반영해야겠고, 상대적으로 분류 확률이 낮은 판별기의 의견은 낮게 반영하여 최송 판별기를 만들때 보다 우수하게 만드는것이 목표다.
지금까지 간단하게 Boosting에 대해 알아보았다.
그럼 지금부터 가장 기초인 AdaBoost(아다 Boost)에 대해 알아보자.
2. Ada Boosting(Adaptive Boosting)
Ada Boost는 가장 Boosting기법을 이해하기 쉬운 알고리즘이다.
해당 글 맨 처음 DT(Decision Tree)에 대해 자세히 알고 오라는 말을 봤을 것이다.
이유는, Ada Boost도 DT를 사용하기 때문이다. (Tree 짱...!)
AdaBoost는 깊이(depth)가 1인 DT를 N개 사용하는 알고리즘이다.

이러한 'Stump' 라고 부르는 깊이 1인 DT를 만들어 단순 이진 분류를 통해 어떤 data sample을 맞추고 틀렸는지 판단한다.
(물론 split feature 선택과 경계면은 DT의 'best'방식으로 진행한다. - DT할때 했으므로 생략)
그 후 Amount of say를 구하여 해당 Stump의 영향력을 구하게 된다.(estimator_weight)
Amount of say 공식은 아래와 같다. (2진 분류일 경우)

정답률 / 오답률을 통해 Stump의 영향력을 구했으면, data sample의 weight를 변경해 줘야 한다.

잘 정답으로 분류된 값과, 오분류된 값의 weight를 위와같은 식으로 각각 업데이트를 진행한다.
즉, 오분류된 data sample의 weight는 증가하게 되어 다음 Stump에서 Gini 계수에 영향을 보다 많이 주게 된다.
Gini 계수의 영향을 많이 주다보니, 해당 sample를 구분할 가능성이 높아지게 된다.
Amount of say를 구하고, sample weight조정을 반복하며 N개의 Stump를 만들게 된다.
최종적으로는 각각 Stump 고유의 Amount of say(estimator_weight)의 값을 각각 Stump에 곱한 후, 모두 더하는 앙상블이 진행되게 된다.
이것이 Ada Boost의 원리이다. 아주 간단하지 않은가?
여기까지가 기본적은 Ada Boost의 내용이다.
추가로 밑 링크의 pdf파일은 아주 정리가 잘되어 있으니 반드시 참고 :)
http://dmqm.korea.ac.kr/activity/seminar/323
하지만, 이론은 이론일뿐... 실제 sklearn에서는 어떻게 구현이 되어있을까?
이론과 sklearn에서 구현된 Ada Boost의 차이점을 한번 살펴보겠다.
1. Amount of say 공식의 차이
Amount of say는 해당 Stump의 영향력을 나타내는 지표로, Sample Weight를 변경하는데도 사용되는 아주 중요한 공식이다.
sklearn에서는 위 식과는 다르게 SAMME, SAMME.R이라는 알고리즘을 사용한다. 한번 살펴보겠다.


[코드 1,2]는 sklearn에서 사용하는 Amount of say의 식이다. 이론적인 설명과 조금 다르다.
왜 해당 공식이 다르냐면.. 처음에 말한 Boosting의 조건과 관련이 있다고 한다.
Boosting을 하기위해 약분류기는 반드시 찍는(50%) 수준의 성능보다 높아야 한다고 말했다.
하지만, 이건 2진 분류일때 소리이고.. N진 분류라고 생각하게 된다면 1/N 확률보다 높은 정답률을 생성하는 Stump를 만들어야 하는 것이다.
N의 숫자가 높아지면 높아질수록, 1/N의 확률보다 높은 정확도를 가진 Stump를 만들 수 없어 자칫하면 adaBoost의 학습이 잘못된다고 한다.
그래서 나온것이 SAMME 알고리즘이다.
https://hastie.su.domains/Papers/SII-2-3-A8-Zhu.pdf
해당 링크는 SAMME, SAMME.R 알고리즘 논문이다. 궁금하면 한번 봐보길..
SAMME 알고리즘은 [사진 1]의 Amount of say를 구하는 식과 거의 유사하다. 하지만, np.log(n_classes -1)의 식을 통해 기존 알고리즘의 단점을 개선했다고 볼 수 있다. 어떤 단점을 극복했는지 알아보자.
해당 논문에서 표를 하나 볼 수 있다.


위 그래프를 한번 살펴보자.
둘다 Test Error율이 0.5보다 크다. 즉, 2진 분류일때 오답률이 더 높은 상황이다.
왼쪽(기존 식)은 오답률이 더 높아 횟수를 많이 해도 AdaBoost의 학습이 진행되지 않는다.
반면, SAMME는 똑같이 Test Error율이 0.5이상이였지만, 왼쪽과는 다르게 횟수가 많아질 수록 Error율이 떨어지는, 학습하는 모습을 볼 수 있다.
즉, SAMME알고리즘을 사용했을때 Test Error가 1 -(1/n)보다 높더라도 학습을 진행할 수 있는 장점이 생기게 된다.
그렇기에 sklearn에서도 사용하고 있는것 같다.
그럼 SAMME.R은 무엇인가?? SAMME알고리즘의 변형으로 [코드 2]와 같다.
SAMME.R은 확률값을 이용해 Amount of say(estimator_weight)를 구한다.
여기서 SAMME와 SAMME.R의 특이한 차이점이 하나 존재한다.
바로, SAMME는 estimator_weight를 각 Stump에 곱하여 앙상블하지만, SAMME.R은 모든 Stump의 중요도를 1로 놓고 앙상블한다. 이유는.. SAMME.R은 각 class의 확률을 구하여 사용하기 때문이라고 생각한다.(이미 확률값에 estimator_weight가 적용된 상태다 - 개인적 생각)
그럼, 마지막으로 sklearn AdaBoost의 parameter를 살펴보고 넘어가도록 하겠다.
estimator : base가 되는 판별기, default = max_depth가 1인 DT(Decision Tree)
n_estimators: Sequential하게 연결할 estimator 갯수
learning_rate : SAMME,.R에서 learning_rate를 곱하는 부분이 있는데 변경가능, defalut = 1.0
algorithm : { SAMME, SAMME.R } default = SAMME.R
random_state: 재현성을 위한 랜덤값 고정
base_estimator: 1.2version부터 사라짐. estimator로 대체
별로 살펴볼 파라미터는 존재하지 않는 것 같다.
여기까지 Boosting이란 무엇이고, Boosting을 적용한 가장 쉬운 알고리즘인 AdaBoost를 살펴보았다.
Boosting에서 챙겨야할 필수 개념(Amount of say, sample_weight, Sequential)은 기억해두면 좋을 것이다.
'머신러닝' 카테고리의 다른 글
| [ML] GBM(Gradient Boosting Machine) - (1) 실제 학습, 예측 방법 (0) | 2023.03.22 |
|---|---|
| [ML] GBM(Gradient Boosting Machine) - 정리 (0) | 2023.03.21 |
| [ML] Decision Tree vs Random Forest vs Extra Tree 표 비교 (0) | 2023.02.28 |
| [ML] Extra Tree (Extremely Randomized Trees)- 정리 (0) | 2023.02.28 |
| [ML] Random Forest - 정리 (0) | 2023.02.28 |
- Total
- Today
- Yesterday
- 욜로
- LLM
- 파이썬
- 오류
- 초보자
- 어탠션
- c3k2
- 오블완
- YOLOv8
- python
- 딥러닝
- DeepLearning
- 깃
- 이미지
- GIT
- 도커
- 정리
- yolov11
- 알고리즘
- 뜯어보기
- Tree
- github
- GNN
- docker
- CNN
- 자바
- java
- 티스토리챌린지
- V11
- YOLO
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
