티스토리 뷰
지금까지 Decision Tree의 분류/회귀가 어떻게 동작하는지 알아보는 시간을 가졌다.
혹시 잘 모른다면 밑에 링크를 통해 보고 오는 것을 추천한다.
https://sims-solve.tistory.com/89
[ML] 의사결정트리(Decision Tree) - Classicifation 손으로 구하기
이번 포스팅에는 직접 Decision Tree가 어떤 방식으로 분기하는지 그림으로만 보는 것이 아닌, 손으로 계산하여 정말 똑같은지 확인해보고자 한다. 만약, Decision Tree에 대해 잘 모르겠다면.. 정보를
sims-solve.tistory.com
https://sims-solve.tistory.com/90
[ML] 의사결정트리(Decision Tree) - Regression 손으로 구하기
이번 포스팅에는 직접 Decision Tree의 Regrssion을 살펴보자! 이전 포스팅과 마찬가지로 손으로 한번 간단한 dataset을 가지고 직접 구해보겠다. 만약, Decision Tree Classification을 모른다면, 밑에 링크를 참
sims-solve.tistory.com
그럼 분명 Decision Tree의 단점이 존재할 것이다. 과연 무엇일까?
바로, 모든 데이터를 끝까지 분류, 회귀할 수 있을때까지 Tree를 구성하게 된다.
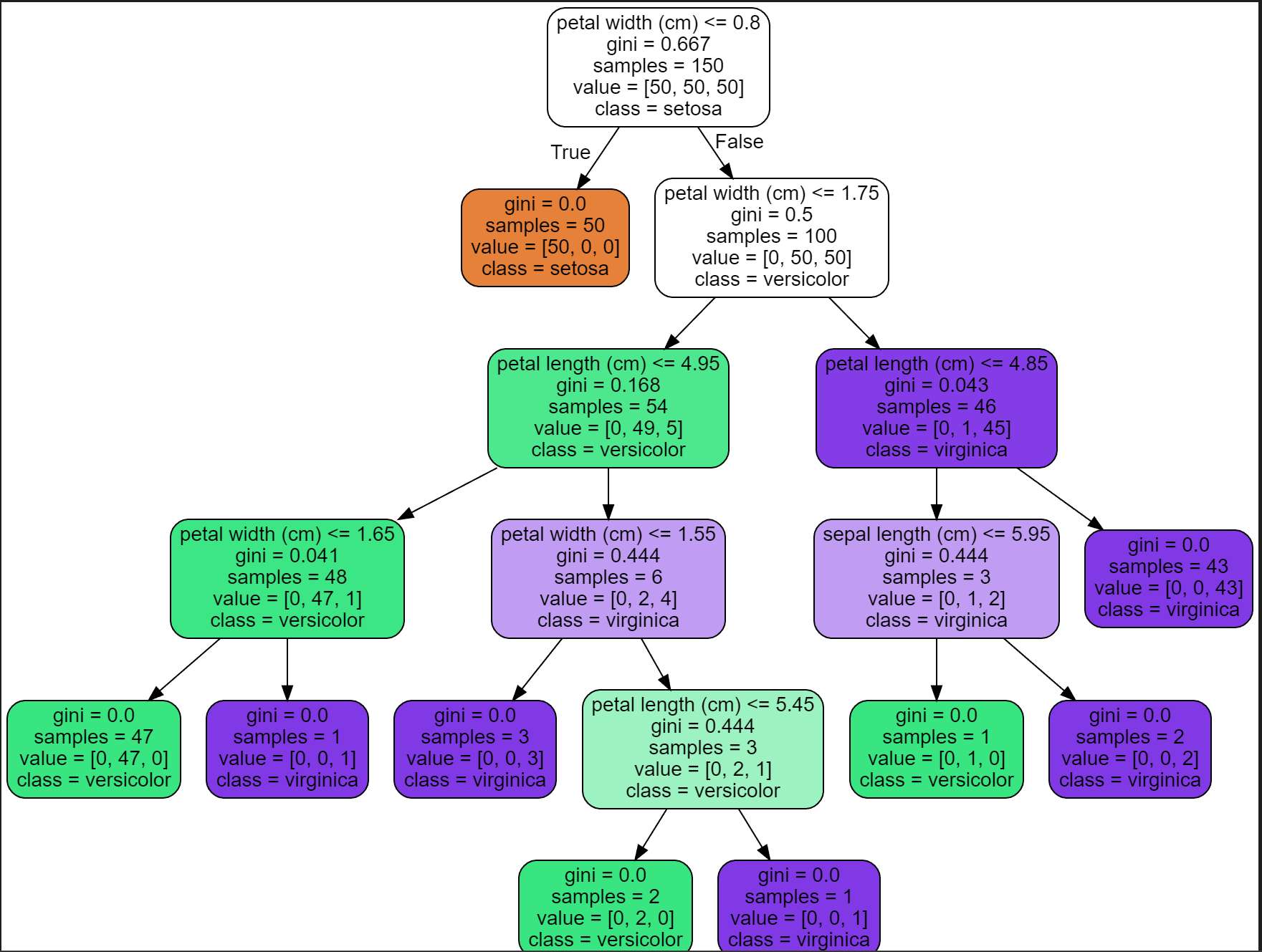
이와같이 leaf node들을 보면 다 gini 계수가 0인걸 확인할 수 있다. 이진으로 나누기때문에 언젠가는 다 다눌수 있을것이고, 그렇게 된다면... 엄청 과적합된 모델이 나올것이라, test 데이터 셋에서는 무용지물이 될 수 있다.
이걸 방지하고자 나오는 방식이 오늘 포스팅의 주된 내용인 pruning (가지치기) 이다.
단어 뜻 그대로, Split 하는걸 방지하여 과적합을 방지하는 것이다.
그럼, 이쯤되서 Decision tree의 공식문서를 한번 살펴보자.
criterion : {“gini”, “entropy”, “log_loss”}, default=”gini” > 어떤 방식으로 불순도를 구할것인가
splitter : {“best”, “random”}, default=”best” > 가장 최적의 경계선을 찾을것이나 랜덤으로 찾을것이냐
max_depth : int, default=None > Tree의 최대깊이
min_samples_split : int or float, default=2 > Split 수행하기 위한 최소 샘플 수
min_samples_leaf : int or float, default=1 > leaf node에서의 가져야할 최소 sample 수
min_weight_fraction_leaf : float, default=0.0 > ?
max_features : int, float or {“auto”, “sqrt”, “log2”}, default=None > split 구간을 찾을 feature 수
random_state : int, RandomState instance or None, default=None > 무작위성 (재현성을 위한 파라미터)
max_leaf_nodes : int, default=None > leaf node의 최대 수 (즉, 총 몇개의 leaf node로 제한)
min_impurity_decrease : float, default=0.0 > IG 값이 해당 값보다 높을때 split (즉, IG가 최소 이정도 이상 될때 split)
class_weight : dict, list of dict or “balanced”, default=None > dictionary 형태로 각 클래스별 weight를 적용시킬시,
gini를 구할때 해당 클래스 데이터 수 * 비율을 곱한것으로 계산
ex ) 1 = 3개 , 2 = 4개 인경우 class_weight를 {1:0.5, 2:2}로 지정을 하면.. Gini 계수 구하는 방식은
Gini : 1 - ( (3 * 0.5) / (3 * 0.5 + 4 * 2) + (2 * 2) /(3 * 0.5 + 4 * 2) ) 로 불순도를 구한다.
ccp_alpha : non-negative float, default=0.0 >
위와같이 Decision Tree의 파라미터가 존재하는걸 볼 수 있다.
이러한 파라미터들을 잘 사용하여 Tree의 형태를 규제시켜 일반화된 성능을 뽐낼 수 있도록 해야한다.
max_depth , min_samples_split , min_samples_leaf , max_leaf_nodes 등.. 사용하여 데이터셋에 오버피팅이 되지 않도록 방지하는 것이 pruning 가지치기 기법이다.
한가지 예제를 들어보겠다.

[사진 2]에서 leaf node를 보면 모두 하나의 class만 들어있는걸 볼 수 있다.
현재, depth는 5이다. 하지만 여기서 한번 max_depth를 3으로 지정해보겠다.

이와같이 depth가 3인 tree가 만들어졌고, [사진 2]와는 다르게 leaf node에 서로다른 class가 섞여있다. (이럴경우 가장 많은 class를 정답이라고 판단)
이번에는 min_samples_leaf 5로 지정하여 진행해보겠다.

위와같은 결과가 나오는데, 여기서 leaf node의 sample 수를 보면 모두 5이상인걸 볼 수 있다.
이처럼 tree에 파라미터를 조절하여 tree에 제약을 걸고, 오버피팅을 방지하는게 일반적인 성능을 낼 수 있도록 만들어준다.
자, 지금까지 Decision Tree에 대해 정말 자세하게 살펴보았다.
하지만, 맨 처음 말했 듯 Decision Tree는 Tree기반 알고리즘 내부에 사용되는 모델이다. 다른 상위 모델을 보기위한 초석에 불과하다.
다음에는 드디어 Random Forest에 대한 포스팅을 하겠다.
Decision Tree에 대한 내용을 모두 이해했으니, Random Forest는 빠르게 넘어갈 수 있을것이다.
'머신러닝' 카테고리의 다른 글
| [ML] Extra Tree (Extremely Randomized Trees)- 정리 (0) | 2023.02.28 |
|---|---|
| [ML] Random Forest - 정리 (0) | 2023.02.28 |
| [ML] 의사결정트리(Decision Tree) - Regression 손으로 구하기 (0) | 2023.02.25 |
| [ML] 의사결정트리(Decision Tree) - Classification 손으로 구하기 (0) | 2023.02.25 |
| [ML] 의사결정트리(Decision Tree) 정리 (0) | 2023.02.25 |
- Total
- Today
- Yesterday
- YOLOv8
- c3k2
- 딥러닝
- YOLO
- 초보자
- GNN
- 알고리즘
- GIT
- github
- 파이썬
- 어탠션
- 뜯어보기
- yolov11
- 오류
- Tree
- 티스토리챌린지
- LLM
- 오블완
- python
- 욜로
- CNN
- 이미지
- V11
- java
- 깃
- docker
- 자바
- 도커
- DeepLearning
- 정리
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
